【Numpy&Matplotlib】相関プロットでエラーバーと回帰直線を表示しよう
こんにちは!
エラーバーはデータの不確実性を示すため、データを示し際には重要です。
今回は、エラーバーを表示する方法をpythonを用いて実装したいと思います。
相関プロット
相関プロットは、高校数学のデータの分析においてよく見たグラフだと思います。
相関係数によって、比較対象の2つの要素の関係がわかります。
データの準備
まずは、以下の2つをインポートします。
'''
import numpy as np
import matplotlib.pyplot as plt
'''
numpy: 計算ツール
matplotlib: 描写ツール
xとyのデータと、それぞれの標準偏差の
データを用意します。
'''
x = np.arange(1,12,1) #1
y = np.array([2,3,6,5,10,10,12,14,18,20,20]) #2
x_err = np.array([0.6, 0.6, 0.6, 0.6, 0.7, 0.9, 0.7, 0.9, 0.8, 0.2, 0.5])
y_err = np.array([0.6, 0.7, 0.5, 0.8, 0.5, 0.3, 0.2, 0.3, 0.6, 0.9, 0.7])
'''
1) np.arange(開始の数, 終りの数, 間隔)
2) np.array([list]) リストをArrayにする。
エラーバー
今回、エラーバーはデータの標準偏差(Standard Deviation)を使います。
#相関係数計算 corr = np.corrcoef(x,y)
相関係数の計算は、np.corrcoef(xのデータ,yのデータ)
でできます。xとyの要素数は揃えないと計算ができません。
corrは配列で出力されます。
⇒array([[1. , 0.9852236],
[0.9852236, 1. ]])
したがって、相関係数は、
corr[0, 1] corr[1, 0]
のどちらかとします。
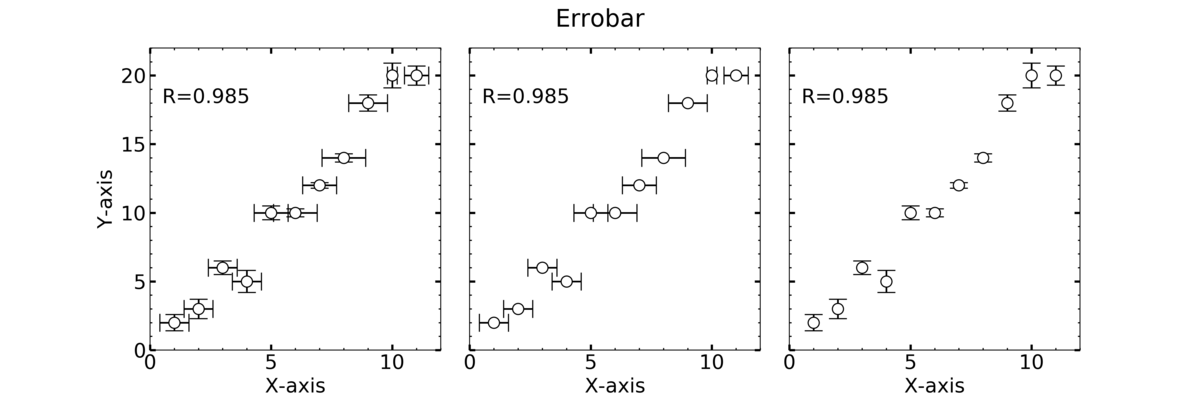
グラフ作成
グラフを書いてみます。
fig = plt.figure(figsize=(15,5))
plt.rcParams["font.size"] = 18
plt.suptitle("Errobar")
ax1 = plt.subplot(131)
ax2 = plt.subplot(132)
ax3 = plt.subplot(133)
ax1.errorbar(x, y, xerr=x_err, yerr=y_err, fmt = "o"
,markersize = 10,color="k", markerfacecolor="w",capsize=8)
ax2.errorbar(x, y, xerr=x_err, fmt = "o"
,markersize = 10,color="k", markerfacecolor="w",capsize=8)
ax3.errorbar(x, y, yerr=y_err, fmt = "o"
,markersize = 10,color="k", markerfacecolor="w",capsize=8)
axes = [ax1, ax2, ax3]
for ax in axes:
#範囲の設定
ax.set_xlim(0, 12)
ax.set_ylim(0, 22)
#メモリの設定
ax.minorticks_on() #補助メモリの描写
ax.tick_params(axis="both", which="major",direction="in",length=5,width=2,top="on",right="on")
ax.tick_params(axis="both", which="minor",direction="in",length=2,width=1,top="on",right="on")
#ラベルの設定
ax.set_xlabel("X-axis")
ax.set_ylabel("Y-axis")
#テキストの貼り付け
ax.text(0.5, 18, "R={:.3f}".format(corr[0,1]))
ax.label_outer()
plt.subplots_adjust(wspace=0.1)
plt.show()
#保存
fig.savefig("XXX.png",format="png", dpi=330)
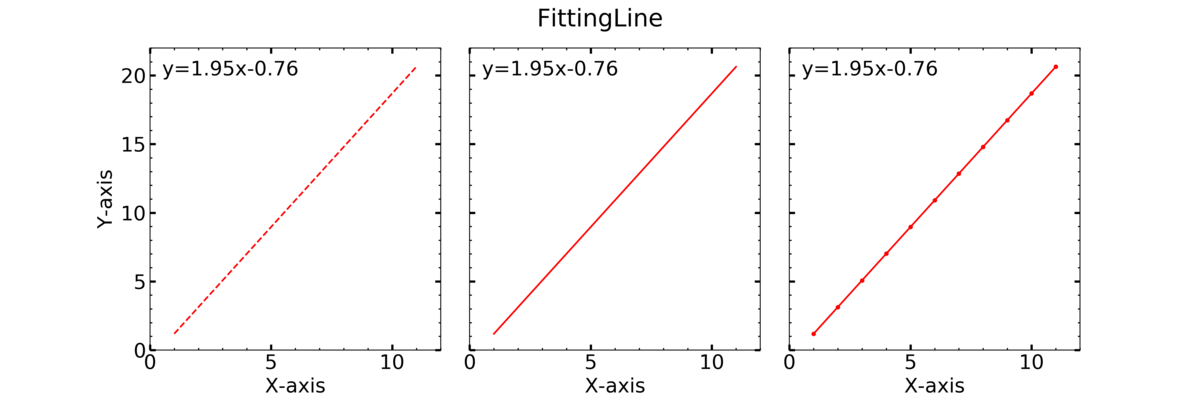
回帰直線
1次の回帰なので、y=ax+bが求める回帰直線です。 以下の操作で計算できます。
#回帰直線 p = np.polyfit(x, y, 1) y_reg = x*p[0]+p[1]
np.polyfit(xのデータ, yのデータ, 次元)
p[0]=傾き
p[1]=切片
グラフ作成
グラフを書いてみます。
fig = plt.figure(figsize=(15,5))
plt.rcParams["font.size"] = 18
plt.suptitle("FittingLine")
ax1 = plt.subplot(131)
ax2 = plt.subplot(132)
ax3 = plt.subplot(133)
ax1.plot(x, y_reg, "--" ,color="r")
ax2.plot(x, y_reg, "-" ,color="r")
ax3.plot(x, y_reg, ".-" ,color="r")
axes = [ax1, ax2, ax3]
for ax in axes:
#範囲の設定
ax.set_xlim(0, 12)
ax.set_ylim(0, 22)
#メモリの設定
ax.minorticks_on() #補助メモリの描写
ax.tick_params(axis="both", which="major",direction="in",length=5,width=2,top="on",right="on")
ax.tick_params(axis="both", which="minor",direction="in",length=2,width=1,top="on",right="on")
#ラベルの設定
ax.set_xlabel("X-axis")
ax.set_ylabel("Y-axis")
#テキストの貼り付け
ax.text(0.5, 20, "y={:.2f}".format(p[0])+"x{0:+.2f}".format(p[1]))
ax.label_outer()
plt.subplots_adjust(wspace=0.1)
plt.show()
#保存
fig.savefig("XXX.png",format="png", dpi=330)
相関グラフまとめ
def main():
fig = plt.figure(figsize=(10,10))
plt.rcParams["font.size"] = 18
ax = plt.subplot(111)
ax.errorbar(x, y, xerr=x_err, yerr=y_err, fmt = "o"
,markersize = 10,color="k", markerfacecolor="w",capsize=8)
ax.plot(x, y_reg, color="r")
#範囲の設定
ax.set_xlim(0, 12)
ax.set_ylim(0, 22)
#メモリの設定
ax.minorticks_on() #補助メモリの描写
ax.tick_params(axis="both", which="major",direction="in",length=5,width=2,top="on",right="on")
ax.tick_params(axis="both", which="minor",direction="in",length=2,width=1,top="on",right="on")
#ラベルの設定
ax.set_title("Correlation")
ax.set_xlabel("X-axis")
ax.set_ylabel("Y-axis")
#テキストの貼り付け
ax.text(0.5, 20, "y={:.2f}".format(p[0])+"x{0:+.2f}".format(p[1]))
ax.text(0.5, 18, "R={:.3f}".format(corr[0,1]))
plt.show()
#保存
fig.savefig("XXX.png",format="png", dpi=330)
if __name__ == "__main__":
main()

参考
それでは 🌏