【データ解析】Pythonでデータ解析[基礎]ー数と文字・計算・配列・行列

こんにちは

今日はpythonでデータ解析の基礎です

数と文字

主に用いられる型(type)

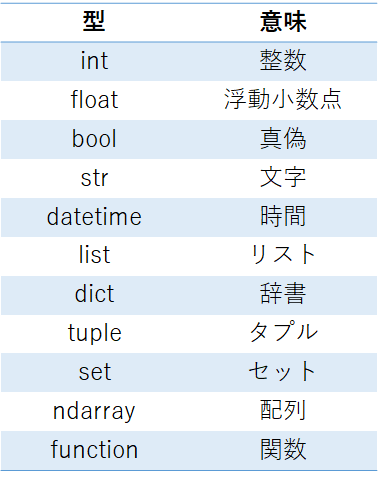
 整数(int)

a = 4
type(a)
>>>int

 浮動小数点(float)

b = 4.4
type(b)
>>>float

b2 = 1/3
type(b2)
>>>float

 真偽(True or False)

c = True
type(c)
>>>True

文字列(str)

d = "NAME"
type(d)
>>>str

日付(datetime)

import pandas as pd
e = pd.to_datetime("2019-01-01 12:30")
print(e)
type(e)
>>>2019-01-01 12:30:00
pandas._libs.tslibs.timestamps.Timestamp

リスト(list)

f = [1, 2, 3, 4]
type(f)
>>>list

 辞書

g = {"A1":1, "A2":2, "A3":3, "A5":4}
type(g)
>>>dict

タプル

h = (1, 2, 3, 4)
type(h)
>>>tuple

セット

i = {1, 2, 3, 4}
type(i)
>>>set

配列(array)

import numpy as np
j = np.arange(1,5,1)
type(j)
>>>numpy.ndarray

関数

def my_name(name):
    print(name)
my_name("Alex")    
type(my_name)
>>>Alex
function

計算

 基本的な計算から、行列計算までです

加法・減法・乗法・除法

1 + 4
>>>5

4 - 1
>>>3

11 * 12
>>>132

33 / 3
>>>11.0

11 % 2
>>>1

配列

 np.arange(x, y, n)

xからyまでのn間隔の配列の作成

注意するのは、y-1しか数が並ばないこと。

a = np.arange(1, 10, 1)
a
>>>array([1, 2, 3, 4, 5, 6, 7, 8, 9])

a2 = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9])
a2
>>>array([1, 2, 3, 4, 5, 6, 7, 8, 9])

.reshape(行, 列)で配列の次元を変更できます。

#2次元配列作成
b = np.arange(1, 51, 1).reshape(5, 10)
b
>>>array([[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
 [11, 12, 13, 14, 15, 16, 17, 18, 19, 20],
 [21, 22, 23, 24, 25, 26, 27, 28, 29, 30],
 [31, 32, 33, 34, 35, 36, 37, 38, 39, 40],
 [41, 42, 43, 44, 45, 46, 47, 48, 49, 50]])

.reshape(-1,)で1次元配列に戻せます

b2 = b.reshape(-1,)
b2
>>>array([ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,
 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34,
 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50])

最後に配列の情報を確認しておきましょう。

print(b.shape) #配列の形
print(b.ndim) #配列の次元
print(b.size) #配列のサイズ
>>>(5, 10)
>>>2
>>>50

行列計算

基礎

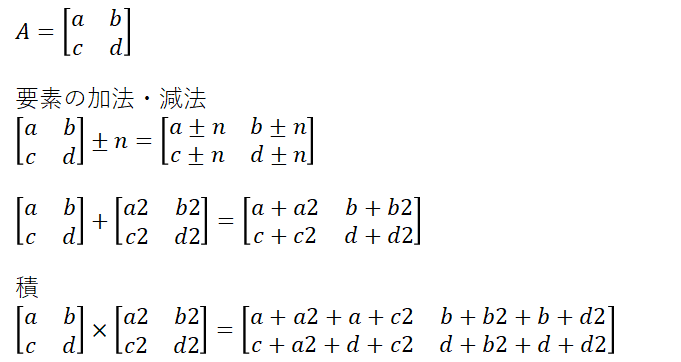
A = np.array([[2, 2], [2, 4]])
A
>>>array([[2, 2],
 [2, 4]])

A + 10
>>>array([[12, 12],
 [12, 14]])

A + A
>>>array([[4, 4],
 [4, 8]])

A * 3
>>>array([[ 6, 6],
 [ 6, 12]])

 ※行列の掛け算ではなく、要素の掛け算である

A * A
>>>array([[ 4, 4],
 [ 4, 16]])

行列の積(3種類の計算方法)

A @ A
np.dot(A, A)
A.dot(A)
>>>array([[ 8, 12],
 [12, 20]])

転置行列・逆行列・単位行列

np.transpose(A)
>>>array([[2, 2],
 [2, 4]])

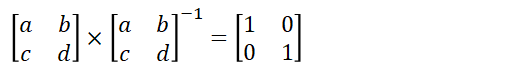
inv_A = np.linalg.inv(A)
inv_A
>>>array([[ 1. , -0.5],
 [-0.5, 0.5]]) 

A.dot(inv_A)
# np.dot(A, inv_A)
>>>array([[1., 0.],
 [0., 1.]])

逆行列が求まらない場合は単位行列は出ない

B = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) B
>>>array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])

#逆行列
inv_B = np.linalg.inv(B)
inv_B
>>>array([[ 3.15251974e+15, -6.30503948e+15, 3.15251974e+15],
 [-6.30503948e+15, 1.26100790e+16, -6.30503948e+15],
 [ 3.15251974e+15, -6.30503948e+15, 3.15251974e+15]])

#元の行列×逆行列
B.dot(inv_B)
>>>array([[ 0. , 1. , -0.5],
 [ 0. , 2. , -1. ],
 [ 0. , 3. , 2.5]])

 ⇑単位行列が求まっていない

それは、元の行列の行列式≠0を満たしていないからである

int(np.linalg.det(B))
>>>0

 行列式

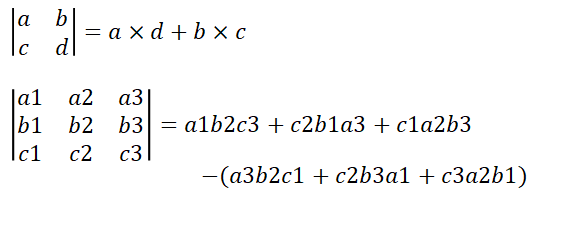
 np.linalg.det(A)
>>>4.0

固有値と固有ベクトル

A = np.array([[2, 2], [2, 4]])
A
>>>array([[2, 2],
 [2, 4]])

w, v = np.linalg.eig(A)
print(w) #固有値
print(v) #固有ベクトル
>>>[0.76393202 5.23606798]
[[-0.85065081 -0.52573111]
 [ 0.52573111 -0.85065081]]

 それでは🌏